Introduction

The length of structures on outcrops which can be maped only provides a two dimensional view on three dimensional extension, therefore the outcrop trace length of a structure is just a more or less plain cut through the structural network contained in a certain rock mass. The map scale also bias the information e.g. aerial maps on large scale neglect all smaller structures (meter or centimeter scale). To have an suitable tool for extrapolating structures into the outofsight rock mass and to compare structures on large scale with those of small scale it was assumed that there is a certain selfaffinity. This selfaffinity can be expressed by using the fractal calculations. In fact this sounds quite promising, but nevertheless it should be handled with care. In literature, often a simple correlation of linear regression better than R² = o,9 is used to show evidence for fractality. Under certain circumstances one can do likewise, but it is not seldomly seen, that data, which is not statisticaly distributed around the regression line, but with a distinct trend (e.g. curved) was published as fractal behavior. If extrapolating this datasets the deviation is increasing.

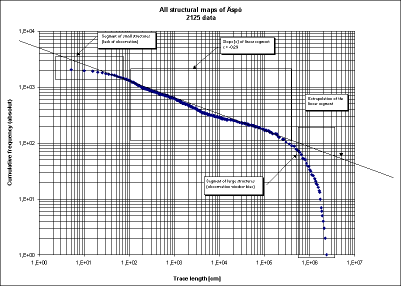
Cumulativ frequency plot of fracture tracelength